Article écrit par Nicolas Zermati
CodinGame est un site web proposant des challenges de programmation. Ces évènements ont pour but de mettre en relation entreprises et postulants au travers de leur code. Cependant, il est tout à fait possible de participer juste pour le fun.
Le challenge se déroule à une date donnée et se compose de plusieurs petits programmes qu’il faut réaliser les uns après les autres.
Les programmes peuvent être écrits en C, C++, Java, C#, PHP, Python ou Ruby. Un IDE en ligne permet d’écrire son code et de le tester avec des jeux de données fournis.
Cependant je pense que beaucoup de participants codent en local, dans leur éditeur favori avant de soumettre leur solutions dans l’IDE.
Dans cet article, je vous propose de reprendre le troisième exercice proposé lors du CodinGame de janvier, de la même manière que lors de l’article sur la résolution des grilles de Boggle.
Sujet de l’exercice
Note : cette section est une copie du sujet présent sur le site de CodinGame.
Vous travaillez au musée de la Résistance nationale et vous venez d’exhumer des centaines de documents contenant des transmissions codées en Morse.
Le Morse est un codage composé de points et de traits représentant des lettres de l’alphabet. Voici la transciption d’un alphabet en Morse :
A : .-B : -...C : -.-.D : -..E : .F : ..-.G : --. | H : ....I : ..J : .---K : -.-L : .-..M : --N : -. | O : ---P : .--.Q : --.-R : .-.S : ...T : - | U : ..-V : ...-W : .--X : -..-Y : -.--Z : --.. |
Dans les documents, aucun espace n’a été retranscrit pour séparer les lettres et les mots qui se cachent derrière une séquence en Morse. Une séquence décodée peut donc avoir différentes interprétations.
Par exemple, la séquence -....--.-. peut aussi bien correspondre à BAC, BANN, DUC, DU TETE, …
Un être humain est capable de reconnaître le découpage adéquat grâce à sa connaissance de la langue mais pour une machine c’est plus délicat. Pour que votre programme puisse faire l’équivalent vous avez à votre disposition un dictionnaire contenant un ensemble de mots corrects.
Cependant, même avec un dictionnaire, il est possible qu’une séquence puisse correspondre à plusieurs messages valides (BAC, DUC, DU et TETE pourraient être présents dans le dictionnaire de l’exemple précédent).
Votre programme devra déterminer le nombre de messages différents qu’il est possible d’obtenir à partir d’une séquence en Morse et d’un dictionnaire donné.
ENTRÉE :
- Ligne 1 : Une séquence Morse de longueur maximale L
- Ligne 2 : Un entier N correspondant au nombre de mots du dictionnaire
- Les N Lignes suivantes : Un mot du dictionnaire par ligne. Chaque mot a une longueur maximale M et n’apparait qu’une seule fois dans le dictionnaire.
SORTIE :
- Un entier R correspondant au nombre de messages qu’il est possible de générer à partir de la séquence en Morse et du dictionnaire.
CONTRAINTES :
- 0 < L < 100000
- 0 < N < 100000
- 0 < M < 20
- 0 <= R < 263
EXEMPLE :
Entrée
......-...-..---.-----.-..-..-..
5
HELL
HELLO
OWORLD
WORLD
TEST
Sortie
2
- Mémoire RAM disponible : 256Mo
- Durée maximum d’exécution : 6 secondes
- Le programme doit lire les entrées depuis l’entrée standard
- Le programme doit écrire la réponse dans la sortie standard
- Le programme doit fonctionner dans l’environnement de test fourni
Avant de commencer…
Plutôt que d’exécuter les tests sur les serveurs de CodinGame, je préfère le faire en local. En effet, cela évite de surcharger inutilement les serveurs et cela va beaucoup plus vite.
Pour résoudre ce type de petit problème, je rassemble donc dans un même répertoire les fichiers suivants :
in1.txt # Entrées n°1
out1.txt # Sorties attendues pour les entrées n°1
...
script.rb # Script permettant de résoudre le problème
test.sh # Script de testPour chaque fichier d’entrées, test.sh compare les sorties du programme avec les sorties attendues. Bien entendu, il faut que les fichiers respectent les formats suivants :
in[0-9]+.txtpour les fichiers d’entrées etout[0-9]+.txtpour les fichiers de sorties.
Ainsi, vous n’avez qu’à lancer ./test.sh pour avoir le résultat des tests :
Testing scenario #1... success
Testing scenario #3... success
Testing scenario #2... success
Testing scenario #4... successLorsqu’une erreur se produit, la suite de tests est interrompue et un diff est affiché :
Testing scenario #1... failure
1c1
< 1
---
> 2Ici, la réponse attendue est 1 mais la réponse affichée par le script est 2.
Vous trouverez tous les fichiers sur le dépot Github associé à l’article.
Analysons le problème
Commençons par étudier les entrées du problème. On a :
- des lettres en ASCII ainsi que leur équivalent en morse,
- une liste de mots en ASCII et
- une séquence de caractères morse sans séparateurs.
Puisque l’inconnue du problème est en morse autant considérer le dictionnaire comme étant lui aussi en morse. Voila un exemple de code permettant de récupérer les entrées.
$ascii_morse_mapping = {'A'=>'.-', 'B'=>'-...', [...] 'Y'=>'-.--', 'Z'=>'--..'}
$sequence = gets.chomp
$dico = (1..gets.to_i).map do
result = ''
gets.chomp.each_char{ |char|
result << $ascii_morse_mapping.fetch(char) }
result
end
On peut remarquer qu’un mot en morse peut correspondre à des mots différents en ASCII. Par exemple .........- peut se traduire par SHIT ou bien HIV. Ainsi $dico est susceptible de contenir des doublons.
L’objectif est de trouver le nombre de découpages possibles de $sequence en mots de $dico.
Rentrons dans le tas !
Comme je l’avais fait pour la résolution du Boggle, je vais d’abord commencer par un algo naïf.
Dans les fichiers de test 1 et 2, la séquence correspond à un seul et unique mot du dictionnaire. En conséquence, la solution suivante va fonctionner :
$dico.select{|word| word == sequence}.size
L’exemple n°3 se complique : plusieurs mots forment la séquence. On va donc, pour chaque mot, tenter de le faire correspondre avec le début de la séquence. S’il correspond, alors on recommencera l’opération avec le reste de la séquence. Lorsque la séquence est vide, on a une seule interprétation possible.
Cet algorithme se décrit très bien à l’aide d’une fonction récursive :
defpossibilities(seq)
return 1 if seq.size == 0
$dico.reduce(0) do|total, word|
if word == seq[0, word.size]
total += possibilities(seq[word.size, seq.size - word.size])
end
total
end
end
La fonction possibilities donne donc le nombre de combinaisons possibles pour la séquence en paramètre. Lorsque l’on appelle cette fonction avec $sequence en paramètre on a bien le résultat attendu pour les tests 1, 2 et 3. Le test n°4, lui, ne termine pas en en temps acceptable…
Optimisation
Le problème et notre algorithme de résolution peuvent être vus comment un arbre :
- Les nœuds de l’arbre contiennent la séquence dont on cherche à déterminer le nombre d’interprétations.
- Les branches de l’arbre représentent la correspondance d’un mot du dictionnaire en tête de cette séquence.
- Les feuilles de l’arbre sont des nœuds dont la séquence est vide.
La racine de l’arbre contient $sequence. La fonction possibilities(seq) retourne le nombre de feuilles pour une séquence donnée. Le nombre de feuilles est calculé récursivement : c’est la somme du nombre de feuilles de chacun des sous-arbres du nœud.
Voici un exemple de représentation du problème (en ASCII). Dans l’exemple la séquence est ABCD et le dictionnaire est : A, AB, B, BC, C, CD. Ici la séquence est en ASCII plutôt qu’en morse pour plus de lisibilité.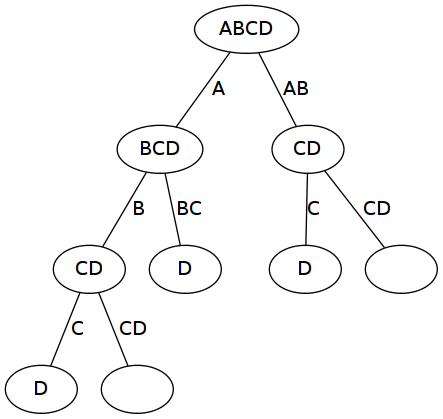
Avec cet exemple l’ordre des appels à la fonction possibilities est le suivant :
possibilities('ABCD') => 2
possibilities('BCD') => 1
possibilities('CD') => 1
possibilities('D') => 0
possibilities('') => 1
possibilities('D') => 0
possibilities('CD') => 1
possibilities('D') => 0
possibilities('') => 1
Sur le graphe comme dans les appels, on remarque qu’on a plusieurs portions identiques. Respectivement, il s’agit des sous-arbres CD et D et des appels à possibilities avec les arguments : 'CD', 'D' ou ''.
Memoize
La fonction possibilities est dite pure. En effet, à l’exception de son usage de la variable $dico que l’on considère plutôt comme une constante, possibilities ne tient pas compte du contexte d’exécution mais uniquement de ses paramètres.. Pour les mêmes paramètres, elle retournera toujours le même résultat.
Cette propriété va nous permettre de conserver en mémoire les résultats des appels à la fonction. De cette manière, on ne calculera pas un sous arbre déjà calculé.
$possibilities_memory = {}
defpossibilities(seq)
return 1 if seq.size == 0
return $possibilities_memory[seq]if $possibilities_memory.has_key?(seq)
result = $dico.reduce(0) do|total, word|
if word == seq[0, word.size]
total += possibilities(seq[word.size, seq.size - word.size])
end
total
end
$possibilities_memory[seq]= result
end
Cette optimisation permet de terminer dans un temps raisonnable l’exemple n°4 (~7 secondes). L’algorithme n’a quasiment pas changé !
Dictionnaire
Pour optimiser à nouveau notre programme, regardons d’un peu plus près son fonctionnement interne. Pour cela, on peut instrumenter le code pour obtenir certaines métriques sur les opérations les plus courantes. On peut également faire une analyse de complexité. Dans cet article je vais utiliser l’instrumentation.
Vous trouverez sur Github une version instrumentée du code précédent. Voici ce que j’obtiens sur l’exemple n°4 :
{ :calls => 1284, # Nombre d'appel à la fonction
:nodes => 1194, # Nombre de sous-arbres parcourus
:cuts => 89, # Nombre de sous-arbres non recalculés
:match => 1283, # Nombre de branches crées
:unmatch => 11274853 } # Nombre de branches non-crées
On peut voir que notre algorithme calcule assez peu de sous arbres (de l’ordre d’un millier). Par contre il fait beaucoup d’essais pour faire correspondre les mots du dictionnaire au début de la séquence (de l’ordre d’une dizaine de millions). Pour chaque nœud calculé on va tester chaque mot du dictionnaire avec le début de la séquence. Il y a 9444 mots dans le dictionnaire, on a donc 9444 * 1194 comparaisons.
Pour éviter de parcourir le dictionnaire à chaque nœud, on va prendre l’approche inverse. On va chercher à faire correspondre le début de la séquence à un mot du dictionnaire. Pour cela on va parcourir le début de la séquence, et vérifier si oui ou non il existe une correspondance dans le dictionnaire.
Pour limiter le nombre d’appel au dictionnaire on ne s’intéresse qu’aux séquences pouvant effectivement être un mot. Cette limite est mise en place en ne prenant que des préfixes de la taille des mots du dictionnaire.
Voici le corps de ce que pourrait être notre nouvelle méthode possibilities.
result = 0
min = $dico.min_size
max =[$dico.max_size, seq.size].min
for size in (min..max)
if $dico.exists?(seq[0, size])
result += possibilities(seq[size, seq.size - size])
end
end
result
L’une des premières choses que l’on remarque c’est que $dico ne semble plus être une simple liste. Comme on l’a vu plus tôt, plusieurs mots peuvent avoir une même représentation en morse. En plus de savoir si un préfixe de seq est dans le dictionnaire, il faut savoir combien de fois il y est. L’algorithme change légèrement afin de prendre en compte ce détail :
result = 0
min = $dico.min_size
max =[$dico.max_size, seq.size].min
for size in (min..max)
count = $dico.count(seq[0, size])
if count > 0
result += count * possibilities(seq[size, seq.size - size])
end
end
result
Voici maintenant le code du dictionnaire :
classDictionnary
def initialize
@_hash = {}
end
def push(morse)
@_max_size =nil
@_min_size =nil
@_hash[morse]= count(morse) + 1
end
def count(morse)
@_hash[morse]|| 0
end
def max_size
@_max_size ||= @_hash.keys.max_by(&:size).size
end
def min_size @_min_size ||= @_hash.keys.min_by(&:size).size
end
end
Cette implémentation permet de résoudre le test n°4 instantanément (~20 millisecondes). Voici les résultats donnés par le même type d’instrumentation que précédemment :{ :calls => 1284, # Nombre d’appel à la fonction :nodes => 1224, # Nombre de sous-arbres parcourus :cuts => 59, # Nombre de sous-arbres non recalculés :match => 1283, # Nombre de branches crées :unmatch => 48901 } # Nombre de branches non-crées
Le nombre de recherches dans le dictionnaire qui n’aboutissent pas est beaucoup moins élevé (il s’agit d’un facteur 1 000).
La différence de sous arbres non recalculé vient probablement de la différence dans l’ordre de parcours. Cette différence laisse penser que l’on pourrait ordonner l’exploration pour maximiser le nombre de sous-arbres non explorés. Ce sera peut être le sujet d’un prochain billet…
Pour plus de lisibilité, le code est refactoré en trois classes : Dictionnary, Word et Problem. Vous pouvez voir l’intégralité du script résultant sur Github.
Mémoire
Un dernière optimisation (pour aujourd’hui) consiste à ne plus utiliser des chaînes de caractères lors des récursions ou lors de la mémoization. En effet, on préférera utiliser un indice associé à une variable d’instance de la classe Problem. De cette manière Problem reste fonctionnel, dans le sens ou le résultats de ses méthodes ne dépendent que de lui et de ses propres variables.
Vous pouvez consulter le code associé à cette optimisation sur Github. Cette version inclut l’instrumentation.
Conclusion
Voila c’est terminé pour ce nouvel exercice de programmation. Comme toujours, j’espère que la lecture de cet article vous aura été agréable. N’oubliez pas que le prochain CodingGame a lieu le 28 mai. Si vous aimez ce genre de petits exercices vous devriez penser à participer.
À lire aussi
Ouidou vous souhaite une très bonne année 2025 !
Challenge technique de noël 2024 inter-agences
Intégration de Hibernate Search avec Spring Boot
