Indexation d’images par le Deep Learning dans le Big Data

Écrit par Yassine Amraoui

Avant de commencer

Le cortex visuel animal a inspiré de nombreux scientifiques et a contribué à la création des modèles de réseaux neuronaux actuels. Parmi les réseaux de neurones existants, nous nous intéresserons à une catégorie très largement utilisée dans la recherche multimédia : les réseaux de neurones convolutifs, aussi appelés CNN (Convolutional Neural Network).

L’objectif de cet article est de présenter les fondamentaux du Deep Learning via le cas particulier des CNN, ainsi que de montrer des idées d’utilisation de l’apprentissage automatique dans la recherche d’images.

C’est quoi le Deep Learning ?

Il s’agit d’une forme d’intelligence artificielle, dérivée du Machine Learning, permettant l’apprentissage automatique.

Basons-nous sur un exemple concret de machine learning afin de comprendre le principe. On part d’une entrée (input) qui est la représentation vectorielle d’une image représentant le chiffre « 1 ». Le but du programme ici est de retrouver la classe de l’image input, à savoir la classe « 1 », parmi les 10 classes existantes (correspondant aux chiffres de 0 à 9).

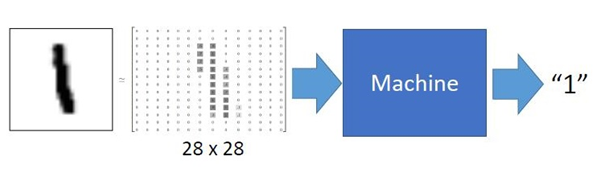
Le programme doit « apprendre » à retrouver la classe de l’image à l’aide d’une base de données d’entraînement correspondant aux chiffres de 0 à 9). Cette base contient des couples formées d’images et de leur labels respectifs. Dans notre exemple précédent, le label d’une image de la base d’entraînement est le chiffre que cette image représente.

Un réseau « entraîné » signifie que ses poids synaptiques sont ajustés de sorte à ressortir, à l’aide d’une fonction d’activation, la bonne classe en sortie. Les poids synaptiques correspondent aux coefficients multiplicateurs des valeurs en entrée. Ces poids sont internes au réseau, et ce sont eux que l’on entraîne lors de la phase d’apprentissage. L’ajustement des coefficients se déroule jusqu’à ce que la machine retourne la bonne classe pour chaque image d’entrée, idéalement. Pourquoi idéalement, parce que concrètement le réseau n’est pas fiable à 100% pour la plupart des prédictions réalisées de nos jours; l’enjeu scientifique est d’améliorer l’état de l’art. L’ajustement des coefficients utilise un algorithme dit de « réduction de perte », basé sur le principe de descente de gradient.

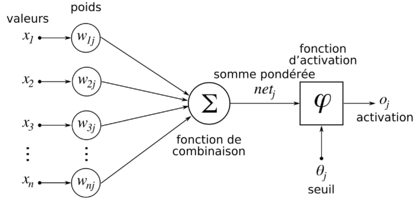
La somme des produits des valeurs d’entrée x(i) avec les poids synaptiques w(ij) renvoie une valeur. Cette valeur passe par une fonction d’activation qui va permettre de savoir si le neurone doit s’activer ou non. C’est exactement ce que l’on appelle la prédiction du neurone : si la valeur est au-dessus d’un seuil fixé, alors la valeur output du neurone sera non nul ; sinon il sera nul (neurone désactivé). Si l’on reprend l’exemple du chiffre « 1 » en tant qu’input et dans le cas d’un réseau entraîné au préalable, le neurone n°0 retournerait 0, le neurone n°1 retournerait 1 et les neurones n°2 à n°9 retourneraient 0 aussi.

L’image ci-dessus représente en fait un seul neurone. Cependant, un réseau de neurone en contient plusieurs. Schématiquement, une série verticale de neurones forment une couche du réseau. Et un réseau de type Deep Learning contient plusieurs couches.

Machine Learning VS Deep Learning

Prenons le cas d’une image requête représentant un dessin de la maison de nos rêves vue de l’extérieur, et que l’on souhaite retrouver dans une grande base de données le top X des images les plus ressemblantes à ce dessin. On peut faire entrer la représentation vectorielle de l’image en tant qu’input dans notre système de couches de neurones.

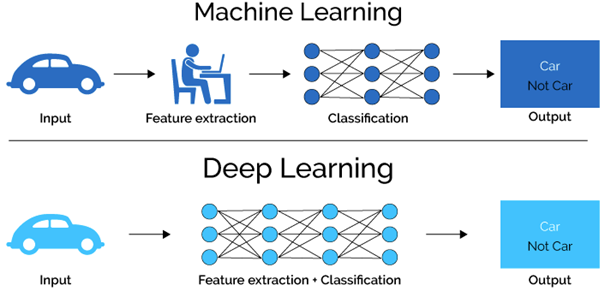
En Machine Learning comme en Deep Learning, on passe d’un input (comme l’image d’une voiture dans la figure ci-dessus) à un output des couches neuronales. Celles-ci transforment un vecteur en un autre. Les vecteurs deviennent plus grands au fur et à mesure que l’on se rapproche de la couche renvoyant l’output : c’est ce que l’on verra par la suite.

Lorsque l’on veut classifier des images plus complexes que des représentations de chiffres, deux couches de neurones ne suffiront pas à retourner un vecteur caractérisant l’image et donc le système ne permettra pas de renvoyer l’output. Un réseau de type Deep Learning dispose donc d’un réseau de couches plus profond que celui proposé par le Machine Learning. Ce grand nombre de couches permet de réaliser une série d’opérations sur l’image input afin de retourner un feature (vecteur caractéristique représentant l’image) tel que les dernières couches du réseau pourront utiliser pour classifier l’image, c’est-à-dire retourner sa classe.

Ainsi, contrairement au Machine Learning, le Deep Learning intègre la partie extraction de features au sein de son réseau, en plus des dernières couches de classification commune aux deux types d’apprentissage automatique.

En Machine Learning, l’input n’est pas forcément l’image en elle-même mais une représentation vectorielle de celle-ci la caractérisant, que l’on appelle un feature. En revanche, en Deep Learning, l’entrée peut être directement l’image puisque le réseau dispose d’un nombre de couches suffisant pour permettre d’extraire les features de l’image.

Les réseaux de neurones convolutifs (CNN)

Un réseau neuronal convolutif est un réseau de type Deep Learning prenant un input -souvent ramené à un vecteur- et retournant un output via des couches de neurones. Ces dernières servent d’extraction de caractéristiques de l’input : on obtient ainsi un (ou des) vecteurs caractéristiques de l’input.

Les CNN sont très utilisés dans la recherche multimédia, en particulier dans la recherche d’images dans le Big Data. Dans un CNN, chaque couche de neurone joue un rôle particulier, bien qu’elles aient toutes un objectif commun : ressortir les traits caractéristiques de l’input afin de ressortir la bonne classe output.

La couche de Convolution

L’image ci-dessus représente une image input symbolisant un « X ». Les pixels dessinant la lettre ont la valeur 1 (ou (255,255,255) en RGB). La couche de convolution va transformer cette matrice input en une autre matrice. Dans une couche de convolution, comme toute couche neuronale, chaque neurone a des poids reliant chaque pixels de l’input à lui-même : ce sont le poids synaptiques vus précédemment. Dans un CNN, ces poids forment ce que l’on appelle des filtres.

Un filtre est donc un ensemble de valeurs visant à « détecter » la présence d’un pattern dans l’image. Dans l’exemple ci-dessus, la matrice en haut à gauche est un filtre visant à savoir si ce qui est dessiné sur celui-ci (un trait blanc en diagonal) est présent sur l’image requête. Pour ce faire, ce filtre va parcourir toute l’image. Le filtre se superpose à l’image et se décale d’un cran à chaque fois, de gauche à droite et de haut en bas, et à chaque étape on note la valeur issue du produit de convolution entre ce filtre et sa superposition sur l’image. La figure ci-dessus représente l’étape où le filtre est à l’endroit où la superposition est « parfaite » (ie. filtre et image ont le même dessin), et donc le produit de convolution donne une matrice de 1, comme l’explique la figure. A chaque décalage du filtre d’un cran, on additionne les valeurs qui composent la matrice résultante, afin d’obtenir une valeur. Lorsque le filtre a parcouru l’ensemble de l’image, on obtient la matrice ci-dessous (à droite) :

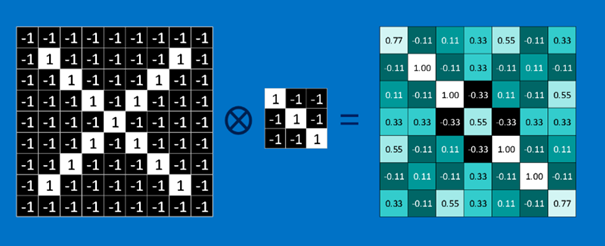
Le filtre a bien détecté la diagonale du « X ». Les filtres qui constituent la couche de convolution vont apporter des informations sur la présence ou non de « formes élémentaires » sur l’image input.

En sortie d’une couche de convolution à N filtres, on obtient une liste de N matrice que l’on appelle des features map. N pouvant être très grand, et la matrice des features map pouvant parfois porter des informations redondantes, il existe des couches qui permettent de réduire la taille des features map : c’est le cas de la couche de Pooling.

La couche de Pooling

Le terme « pooling » signifie en français « mise en commun », et c’est exactement le principe cette couche.

Il existe plusieurs types de Pooling, dont une très connue que l’on appelle Max Pooling, consistant à réduire la taille d’une feature map en prenant la valeur maximale parmi celles sur le cadre parcourant toute la feature (la taille du cadre est fixée au préalable).

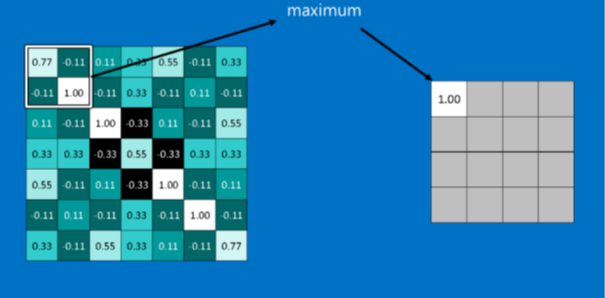
Dans l’exemple de l’image symbolisant un « X », si l’on réalise un Max Pooling sur la feature map présente à gauche, on obtient une feature map plus petite, tout en conservant de l’information sur la présence ou non d’une forme dans l’image. Dans l’exemple ci-dessus, lorsque le cadre (de taille 2*2) aura parcouru toute la feature map (de taille 7*7), on se retrouvera avec une matrice de taille 3 fois plus petite (4*4).

D’ailleurs, il se peut que certaines valeurs soient négatives et ce dès l’entrée dans le CNN. Certaines couches, comme la couche ReLU, traitent ce cas.

La couche de ReLU

Pour chaque valeur x d’une feature map, on la remplace par Max(0,x). Autrement dit, si x est positif alors la valeur reste la même, et si x est négatif la valeur sera remplacée par 0.

Maintenant que l’on a extrait le feature de l’image requête à l’aide des différentes couches, il est possible de classifier l’image à l’aide des informations contenues dans ce feature.

Classification d‘image

Pour la partie classification, soit on part d’une liste de features map, soit on transforme chaque feature map en un vecteur 1D et on concatène toutes ces listes pour obtenir un feature d’une seule dimension. Ce dernier va passer par la partie classification du CNN -décrite dans la partie Machine Learning- afin de prédire la classe associée à l’image requête.

Recherche multimédia

Principe

La partie extraction de features d’un réseau de type CNN peut servir de base de recherche d’images dans le Big Data.

En effet, lorsque la phase d’entraînement d’un CNN donne un score égal à l’état de l’art (avec la partie classification), on peut utiliser ce CNN pour extraire les features de chaque image de la base de données, comme expliqué dans les parties précédentes.

Ainsi, lorsque l’on veut rechercher dans une base de type Big Data les images les plus ressemblantes à une image input, on passe cette dernière dans le modèle pour lui ressortir un feature -et sa classe par la même occasion- et le but est de retrouver les images de la base de données dont les features sont les « plus proches » du feature requête. L’expression « plus proche » correspond à une métrique que l’on choisit en fonction des besoins. La plus commune est la distance euclidienne.

Un algorithme connu utilisant une métrique de distance est le KNN (K Nearest Neighbours), qui consiste à regrouper les features les plus proches en une région, et de ressortir le top k des features les plus proches d’un feature input dans cette région, via une distance euclidienne par exemple.

L’architecture du moteur de recherche multimédia ressemblerait donc à ceci :

Cas concret d’extraction de features avec VGG16

VGG16 est un réseau neuronal convolutif ayant fait ses preuves dans les plus grandes compétitions dédiées au Deep Learning. Il a 16 couches et 138 millions de paramètres environ.

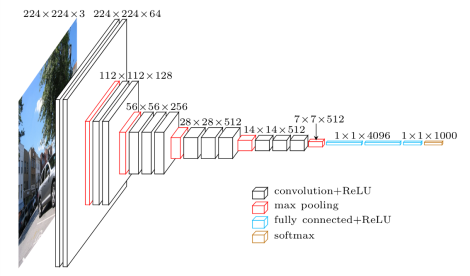
VGG16 dispose des éléments suivants :

• des couches de Convolution avec des filtres 3*3 avec un pas de 1
• des couches de Max Pooling 2*2 avec un pas de 2
• des couches Fully Connected pour aplatir des vecteurs
• des couches ReLU associées à chacune des couches citées
• une couche Softmax pour normaliser le vecteur output provenant de la couche Fully Connected qui la précède

Les deux dernières couches, à savoir Fully Connected et Softmax, sont les couches qui permettent de transformer les features en un vecteur output correspondant à la classe de l’image requête : ce sont donc les couches responsables de la classification dans notre cas.

La dernière couche précédant la couche Fully Connected est une couche de Max Pooling, renvoyant un output de taille 7*7*512. Etant la couche qui est la plus profonde -donc celle qui renvoit les informations les plus précies- et qui ne fait pas partie de la partie classification (mais plutôt de la partie extraction de features), c’est par définition cette couche qui va fournir le feature optimal en output.
De manière générale, dans un réseau neuronal convolutif, on extrait les features depuis l’une des dernières couche d’extraction, juste avant les couches de classification, car ce sont celles qui fournissent les features avec le plus de détails sur l’image requête.

De nos jours, il existe de nombreuses librairies, en particulier en Python, qui implémentent ces couches et les méthodes d’entraînement, de tests et de prédiction. Ce que font la plupart des développeurs c’est se servir de ces codes pour les inclure dans leur projets. Il n’est pas utile de reconstruire son propre réseau neuronal puisque l’état de l’art est déjà à la pointe de la technologie et fournit les meilleurs résultats.

Voici un exemple d’implémentation de VGG16 sous Keras (librairie de Deep Learning Python) :

Ici, la librairie VGG16 est directement importée avec ses poids synaptiques pré-entraînée avec une base de données d’images crée par Google nommée ImageNet. On redimensionne l’image input (‘image_name.jpg’) afin qu’il corresponde à ce que peut recevoir VGG16 en entrée, puis on lance une prédiction de la classe de cette image. En faisant un print(features.shape), on constate que la taille du feature correspond exactement à la taille du vecteur de sortie de la dernière couche de Max Pooling précédemment citée (7*7*512) :

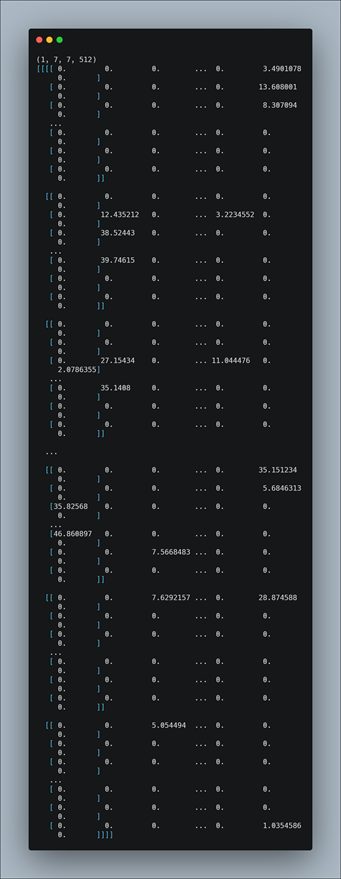
Si jamais le développeur veut extraire les features depuis la couche qu’il désire, il est possible pour lui d’appeler cette couche dans la méthode comme suit :

La couche block4_pool dans VGG16 est l’avant dernière couche de MaxPooling.

Une fois les features extraits de cette façons, il suffit d’implémenter une méthode de distance entre deux vecteurs afin de trouver, parmi les features des images de la même classe que l’image requête, ceux qui sont les plus proches du feature requête.

On peut ainsi développer un moteur de recherche d’images et donc trouver la maison de nos rêves dans une base de données de type Big Data.

Pour aller plus loin

• Analyse des performances d’un réseau de type CNN : courbe rappel/précision
• Optimisation du temps de recherche d’images par une réduction du nombre d’informations d’un feature : méthode R-MAC (Regional Maximum Activation of Convolutions)

Bibliographie

GORDO A., End-to-end Learning of Deep Visual Representations for Image Retrieval [Version électronique], Mai, 1610.07940, (2016)

HUAFENG W, Deep Learning for Image Retrieval : What works and what doesn’t [Version électronique], Juillet, 2015.121, (2016)

KRIZHEVSKY A, ImageNet Classification with Deep Convolutional Neural Networks, Advances in Neural Information Processing Systems 25, Juin, NIPS, (2017)

RUI Y, Image Retrieval : Current Techniques, Promising Directions, and Open Issues, Journal of Visual Communication and Image Representation 10, Avril, 0413.3962, (2017)