Introduction pratique au Q-learning avec Gymnasium Taxi-v3

Écrit par Kévin A.

Introduction

L’apprentissage par renforcement (Reinforcement Learning, ou RL) est une branche de l’intelligence artificielle dans laquelle un agent IA apprend à prendre des décisions par essai-erreur. Contrairement à l’apprentissage supervisé, il n’existe pas de réponses toutes faites : l’agent explore son environnement et améliore ses choix grâce aux récompenses reçues.

Aujourd’hui nous allons découvrir Gymnasium, une bibliothèque open source proposant de nombreux environnements simulés. Dans cet article, nous allons explorer l’environnement Taxi-v3. Dans cet environnement, le but est simple : déplacer le taxi pour récupérer un passager et le déposer à sa destination le plus efficacement possible.

Nous allons découvrir comment entraîner notre agent à accomplir cette tâche en utilisant le Q-Learning, un algorithme à la fois simple et particulièrement efficace.

Comprendre le Q-Learning et la Q-Table

La Q-Table

Le Q-Learning est un algorithme basé sur une Q-Table, une matrice où chaque ligne correspond à un état possible, et chaque colonne à une action. La valeur dans la case Q(s,a) indique la “qualité” de choisir l’action a dans l’état s.

Au départ, la Q-Table est remplie de zéros. L’agent IA apprend progressivement à mettre à jour cette table en interagissant avec l’environnement.

La formule de mise à jour

Chaque fois que le taxi prend une action et reçoit une récompense, la Q-Table est mise à jour selon :

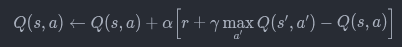
• α (alpha): taux d’apprentissage (généralement entre 0 et 1, mais peut être supérieur dans certains cas spéciaux), correspond au paramètre lr dans notre fonction.
• γ (gamma): facteur d’actualisation qui valorise les récompenses futures, correspond au paramètre gamma dans notre fonction.
• r : récompense immédiate.
• s,a : état et action actuels.
• s′ : nouvel état après action.

Dans notre implémentation, cette formule est appliquée avec les valeurs par défaut de lr = 0.1 et gamma = 0.99, ce qui signifie que l’agent apprend modérément vite et accorde une grande importance aux récompenses futures.

Stratégie d’exploration

Pour éviter que l’agent ne se contente d’une stratégie sous-optimale, on utilise une approche ε-greedy :

L’approche ε-greedy équilibre exploration et exploitation en Q-learning : l’agent explore aléatoirement avec une probabilité ε, sinon il choisit la meilleure action connue. Un ε élevé favorise l’exploration (utile au début), tandis qu’un ε faible privilégie l’exploitation des connaissances acquises.

Le epsilon decay consiste à réduire progressivement la valeur de ε au cours de l’entraînement. Cette diminution graduelle permet de commencer par une exploration intensive pour découvrir l’environnement, puis de converger vers une stratégie stable en privilégiant l’exploitation des connaissances.

Plusieurs approches existent pour implémenter cette décroissance :

• La décroissance exponentielle utilise la formule ε = ε_initial × decay_rate^épisode et offre une réduction rapide au début qui ralentit progressivement.
• La décroissance linéaire applique une réduction constante à chaque épisode avec ε = ε_initial – (decay_step × épisode).
• Une approche particulièrement populaire est la décroissance avec plancher, qui suit ε = max(ε_min, ε × decay_rate) et maintient un niveau minimal d’exploration permanent, évitant que l’agent devienne trop rigide.
• Enfin, la décroissance inverse propose une formule ε = ε_initial / (1 + decay_rate × épisode) pour une décroissance douce et continue.

Chaque approche offre un compromis différent entre vitesse de convergence et maintien de l’exploration, le choix dépendant de la complexité de l’environnement et des objectifs d’apprentissage.

Description du problème

Dans Taxi-v3, le joueur (notre agent IA) contrôle un taxi dans une grille de 5×5 cases. Sa mission est simple : récupérer un passager à un point donné et le déposer à la bonne destination.

L’environnement nous met à disposition tous les éléments nécessaires pour définir le problème d’apprentissage par renforcement de manière claire et structurée.

• États : position du taxi, position du passager (4 emplacements possibles ou “dans le taxi”), et destination (4 emplacements possibles). Cela donne 500 états possibles.
• Actions : 6 choix sont disponibles – se déplacer au nord, sud, est, ouest, prendre un passager, déposer un passager.
• Récompenses :
  • +20 si le passager est déposé au bon endroit.
  • -10 si le taxi tente une mauvaise action (par exemple déposer sans passager).
  • -1 pour chaque pas, afin d’encourager une solution rapide.

Implémentation en Python

Voici une version simplifiée de l’entraînement avec Q-Learning :

import gymnasium as gym
import numpy as np
# Création de l'environnement Taxi
env = gym.make("Taxi-v3")
# Initialisation de la Q-Table
state_space = env.observation_space.n
action_space = env.action_space.n
Q = np.zeros((state_space, action_space))
# Hyperparamètres
alpha = 0.1     # taux d'apprentissage
gamma = 0.6     # facteur d'actualisation
epsilon = 0.1   # exploration
episodes = 10000
# Entraînement
for episode in range(episodes):
    state, _ = env.reset()
    done = False
    while not done:
        if np.random.uniform(0,1) < epsilon:
            action = env.action_space.sample()  # exploration
        else:
            action = np.argmax(Q[state])        # exploitation
        next_state, reward, done, truncated, info = env.step(action)
        # Mise à jour de la Q-Table
        best_next_action = np.argmax(Q[next_state])
        Q[state, action] = Q[state, action] + alpha * (
            reward + gamma * Q[next_state, best_next_action] - Q[state, action]
        )
        state = next_state

Après un entraînement de 10000 épisodes comme dans notre exemple (quelques minutes) le taxi apprend à résoudre efficacement sa mission.

Résultats et analyse

Évaluation de l’agent

Une fois entraîné, l’agent peut être évalué sur plusieurs parties de test. Les métriques typiques sont :

• score moyen par épisode,
• nombre moyen d’étapes nécessaires pour déposer le passager.

En général, après un bon entraînement, l’agent réussit sa mission en moins de 20 étapes.

Visualisation des performances

On peut tracer la progression du score moyen :

import matplotlib.pyplot as plt
# Liste des récompenses obtenues à chaque épisode d'entraînement
plt.plot(rewards_per_episode) 
# Axe horizontal : numéro de l'épisode (de 0 à nombre total d'épisodes)
plt.xlabel("Épisodes") 
# Axe vertical : récompense cumulée par épisode
plt.ylabel("Score moyen") 
# Titre du graphique montrant l'évolution des performances
plt.title("Progression du taxi avec Q-Learning") 
# Affiche le graphique pour visualiser l'apprentissage de l'agent
plt.show() 

Voici par exemple un des graphiques de l’entraînement de notre agent. Ce graphique montre comment notre taxi apprend au fil du temps grâce au Q-Learning.

Plusieurs choses sont affiché sur ce graphique.

l’axe horizontal, chaque point correspond à un épisode d’entraînement, c’est-à-dire une partie que joue notre taxi. Plus on avance vers la droite, plus l’agent a eu d’occasions d’apprendre.

l’axe vertical, on y voit deux choses : En orange, on voit le nombre d’étapes que l’agent met pour terminer une partie. Au départ, ce nombre est très élevé (l’agent échoue souvent et atteint la limite de 200 actions), puis il diminue progressivement à mesure que le taxi apprend à être plus efficace.

En vert, les récompenses obtenues par l’agent, elles vont très loin dans le négatif au départ, puis augmentent et se stabilisent quand le taxi apprend à bien jouer.

La ligne rouge, elle représente l’exploration. Au début, le taxi teste un peu tout au hasard (l’epsilon est élevé). Au fur et à mesure, il explore moins et applique ce qu’il a appris (l’epsilon diminue jusqu’à 0).

Notre graphique illustre l’évolution des récompenses et du nombre de pas, où l’on observe une stabilisation progressive (convergence) des performances lorsque l’agent apprend une stratégie optimale, tandis que l’epsilon décroît vers zéro.

Optimiser les performances de l’algorithme Q-Learning

Une fois l’algorithme fonctionnel, il est intéressant de chercher à accélérer l’apprentissage et les performances finales de notre agent. Cela passe par l’optimisation des hyperparamètres.

Le taux d’apprentissage (lr)

Le taux d’apprentissage détermine l’importance accordée aux nouvelles informations par rapport aux connaissances déjà acquises dans la Q-Table. Dans notre approche, la valeur par défaut est fixée à 0.1 (sur une échelle de 0 à 1). Un taux trop faible entraîne un apprentissage très lent car l’agent intègre difficilement les nouvelles expériences, tandis qu’un taux trop élevé provoque des changements trop brutaux qui effacent les apprentissages précédents.

Le facteur de discount (gamma)

Le facteur de discount détermine quelle importance l’agent accorde aux récompenses futures par rapport à celles qu’il peut obtenir immédiatement. Notre implémentation utilise une valeur par défaut de 0.99 (sur une échelle de 0 à 1). Un gamma faible incite l’agent à rechercher des gains immédiats sans se soucier des conséquences, alors qu’un gamma élevé le pousse à prendre des décisions qui peuvent être moins avantageuses maintenant mais plus bénéfiques à long terme.

La probabilité d’exploration (epsilon)

La probabilité d’exploration équilibre entre l’exploration aléatoire de nouvelles actions et l’exploitation des meilleures actions connues. Notre approche utilise un decay exponentiel avec la formule : epsilon = min_epsilon + (max_epsilon – min_epsilon) * exp(-epsilon_decay * episode).

Nos paramètres sont configurés avec :

• un epsilon initial de 0.3 pour une exploration modérée au début,
• un max_epsilon de 1.0 permettant une exploration maximale si nécessaire,
• un min_epsilon de 0.001 pour une exploitation quasi-totale en fin d’entraînement,
• et un epsilon_decay de 0.1 pour une décroissance progressive.

Cette configuration permet une transition fluide de l’exploration vers l’exploitation, avec un suivi de l’évolution d’epsilon via epsilon_vec pour analyser le comportement de l’agent.

epsilon = 1.0
epsilon_min = 0.01
epsilon_decay = 0.995
for episode in range(episodes):
    ...
    epsilon = max(epsilon_min, epsilon * epsilon_decay) #  Décroissance avec plancher 

Le nombre d’épisodes

• Plus il y a d’épisodes, plus l’agent a de chances de converger.
• Comme nous pouvons le voir sur le graphique d’entraînement, nous atteignons un point de convergence autour de 20 000 épisodes

Comparer les résultats

La meilleure façon de trouver les bons réglages est de tester plusieurs combinaisons et de comparer les courbes de performance. Une approche simple est la recherche par grille (grid search) : tester différentes valeurs de α, γ, ε et observer la convergence.

def grid_search():
    learning_rates = [0.001, 0.01, 0.1]
    gammas = [0.9, 0.95, 0.99]
    epsilons = [0.1, 0.2, 0.3]
    epsilon_decays = [0.001, 0.01, 0.1]
    best_params = None
    best_reward = float('-inf')
    for lr, gamma, epsilon, epsilon_decay in itertools.product(learning_rates, gammas, epsilons, epsilon_decays):
        print(f"Training with lr={lr}, gamma={gamma}, epsilon={epsilon}, epsilon_decay={epsilon_decay}")
        _, mean_reward = train(env=gym.make("Taxi-v3"),
                               episodes=1000,
                               lr=lr,
                               gamma=gamma,
                               epsilon=epsilon,
                               epsilon_decay=epsilon_decay)
        if mean_reward > best_reward:
            best_reward = mean_reward
            best_params = (lr, gamma, epsilon, epsilon_decay)
    print(f"Best parameters: lr={best_params[0]}, gamma={best_params[1]}, epsilon={best_params[2]}, epsilon_decay={best_params[3]}")
    print(f"Best mean reward: {best_reward}")
grid_search()

Cette méthode peut être améliorée en élargissant la plage de valeurs testées pour chaque paramètre et en augmentant la granularité de la recherche.

Limites du Q-Learning

Même si le Q-Learning fonctionne très bien pour un petit environnement comme Taxi, il présente des limites importantes. La scalabilité constitue un problème majeur car la Q-Table grandit de manière exponentielle quand l’espace d’états devient énorme, rendant impossible son stockage en mémoire vive (RAM) pour des environnements complexes.

De plus, l’algorithme souffre d’un manque de généralisation puisqu’il ne peut pas apprendre sur des états qu’il n’a jamais rencontrés auparavant. Enfin, l’exploration ε-greedy reste une approche basique, alors que d’autres méthodes comme l’exploration de Boltzmann ou UCB (Upper Confidence Bound) offrent des stratégies plus intelligentes.

Pour dépasser ces limites, on peut utiliser des réseaux de neurones pour approximer la fonction Q. C’est le principe des Deep Q-Networks (DQN), utilisés dans des environnements beaucoup plus complexes comme les jeux vidéos, la robotique ou d’autres domaines nécessitant une représentation continue des états.

Visualisation de l’agent

Gymnasium permet de visualiser le plateau de jeu avec :

import gymnasium as gym
env = gym.make("Taxi-v3", render_mode="human")
print(env.render())

Nous avons accès à plusieurs valeurs possibles pour le paramètre render_mode. (ansi, rgb_array, rgb_array_list, human).

Pour cet article nous utiliserons le render_mode “human” qui offre la meilleure visualisation graphique interactive en temps réel.

Et voilà notre agent à l’œuvre !

Conclusion

J’espère vous avoir fait découvrir un sujet intéressant à travers cet article. L’environnement Taxi-v3 est un excellent point d’entrée dans l’IA. Il offre une complexité suffisante pour comprendre les mécanismes fondamentaux tout en restant accessible.

Cet exemple pratique nous a donné un aperçu complet de l’apprentissage par renforcement. Nous avons vu la construction de la Q-Table et l’optimisation des hyperparamètres. Nous avons observé comment un agent développe une stratégie optimale par l’expérience seule, sans supervision directe.

Le Q-Learning s’applique concrètement dans plusieurs domaines. Par exemple, l’optimisation de systèmes de recommandation où l’agent apprend à proposer le contenu le plus pertinent. Ou encore la gestion automatique des ressources serveur pour optimiser les performances. Il peut aussi développer des chatbots qui s’améliorent grâce aux retours utilisateurs. Ces applications montrent qu’un algorithme simple peut résoudre des problèmes complexes du monde réel.

Pour approfondir vos connaissances, plusieurs pistes s’offrent à vous. Explorez d’autres environnements Gymnasium plus complexes. Expérimentez avec des variantes comme SARSA. Ou orientez-vous vers le Deep Reinforcement Learning avec les DQN pour des problèmes nécessitant une représentation continue des états.

liens utiles

Le projet :
https://gitlab.tech.ouidou.fr/kevin.aubel/q-learning

Articles similaire:

Q-Learning in Reinforcement Learning – GeeksforGeeks

A Beginner’s Guide to Q-Learning: Understanding with a Simple Gridworld Example

Reinforcement Learning 101

Site avec implementation de Q-learning:
Search | Kaggle

simonescaccia/dqn-Taxi-v3 · Hugging Face

winkin119/q-Taxi-v3 · Hugging Face